7033. Вложенные множества

Петя недавно узнал о понятии множества и вложенности множеств. Он заинтересовался последовательностями S₀ Ê S₁ Ê S₂ Ê … Ê S_n, у которых каждый следующий элемент – подмножество предыдущего, S₀ – некоторое конечное множество {a₁, a₂, …, a_m}.

Петя отметил: каждому из вложенных множеств можно поставить в соответствие целое число H(S) = . Таким образом H(S₀) = 2^m – 1, H(Ø) = 0.

Петя произвольным образом выбрал n чисел: h₁, h₂, …, h_n. Ему стало интересно: сколько существует разных наборов вложенных множеств S₁, S₂, …, S_n при H(S₁) = h₁ (mod 41), H(S₂) = h₂ (mod 41), …, H(S_n) = h_n (mod 41)? К сожалению, Петя сбился со счета, поэтому просит Вас о помощи.

Вход. Первая строка содержит два целых числа n и m (1 ≤ n ≤ 5, 1 ≤ m ≤ 20). Вторая строка содержит n целых чисел h₁, h₂, …, h_n, каждое из которых удовлетворяет условию: 0 ≤ h_k ≤ 40.

Выход. Вывести искомое количество вложенных множеств. Известно, что это число не превосходит 10¹⁸.

Пример входа 1 3 5 7 3 3	Пример входа 2 3 5 7 4 5	Пример входа 3 1 7 3	Пример входа 4 3 10 31 29 17
Пример выхода 1 1	Пример выхода 2 0	Пример выхода 3 4	Пример выхода 4 28

РЕШЕНИЕ

динамическое программирование - маски подмножеств

Анализ алгоритма

Пусть F(n – i, S_i) равно количеству вложенных множеств S_i Ê S_i+1 Ê … Ê S_n, для которых H(S_i+1) (mod 41) = h_i+1, H(S_i+2) (mod 41) = h_i+2, …, H(S_n) (mod 41) = h_n.

Например, F(1, S_n-1) равно количеству вложенных множеств S_n-1 Ê S_n, для которых H(S_n) (mod 41) = h_n. Положим F(0, S_n) = 1 (имеется одно множество S_n без дополнительных ограничений на него).

Тогда количеством вложенных множеств S₀ Ê S₁ Ê S₂ Ê … Ê S_n будет значение F(n, S₀) = F(n, 2^m – 1). Здесь 2^m – 1 является маской множества S₀ = {a₁, a₂, …, a_m}.

Задача решается генерацией всех возможных искомых последовательностей. Для вычисления F(n, S₀) перебираем все подмножества S₁ множества S₀. Для каждого подмножества, для которого H(S₁) % 41 = h₁, далее решаем подзадачу F(n – 1, S₁), которая ищет количество вложенных n множеств, наибольшее из которых равно S₁. Отсюда

F(n, S₀) =

Хранение значений функции F в ячейках массива f[n][2^m] не пройдет по памяти при заданных ограничениях на n и m. Значения F(n – i, S_i) будут ненулевыми только для таких подмножеств S_i, для которых H(S_i) (mod 41) = h_i. Поэтому F(n – i, H(S_i)) можно хранить в f[n – i][ H(S_i) / 41]. И тогда нам достаточно будет массива размером f[n][2^m / 41].

В тестах могут встречаться значения h_i = 0, на их обработку следует обратить внимание.

Пример

1. Существует только один вариант: S₁ = {a₁, a₂, a₃}, S₂ = S₃ = {a₁, a₂}. H(S₁) = 7, H(S₂) = H(S₃) = 3.

2. Такой комбинации вложенных множеств не существует.

3. H({a₁, a₂}) = 2^{1 – 1} + 2^{2 – 1} = 3, H({a₃, a₄, a₆}) = 2² + 2³ + 2⁵ = 4 + 8 + 32 = 44 = 41 + 3, Н({a₁, a₃, a₅, a₇}) = 2⁰ + 2² + 2⁴ + 2⁶ = 1 + 4 + 16 + 64 = 85 = 2 · 41 + 3, Н({a₂, a₃, a₄, a₅, a₆, a₇}) = 2¹ + 2² + 2³ + 2⁴ + 2⁵ + 2⁶ = 2 + 4 + 8 + 16 + 32 + 64 = 126 = 3 · 41 + 3.

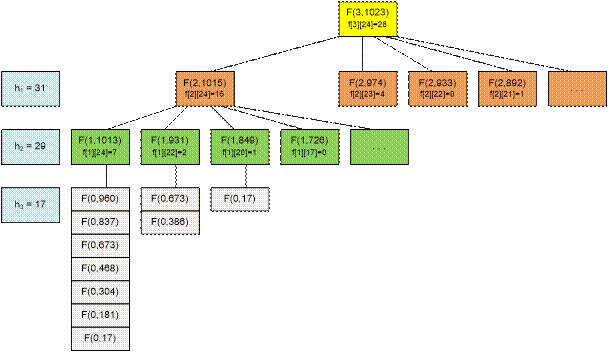
4. Представлено на рисунке.

Реализация алгоритма

Объявим используемые массивы.

int h[5];

long long f[6][(1 << 20) / 41 + 10];

Вычислим значение F(n, mask).

long long F(int n, int mask)

{

if (n == 0) return 1;

int m = mask / 41;

if (f[n][m] != -1) return f[n][m];

f[n][m] = 0;

Перебираем все подмаски sub_mask маски mask. Поскольку возможны h_i = 0, то следует обрабатывать и нулевые подмаски.

for (int sub_mask = mask; ; sub_mask = (sub_mask - 1) & mask)

{

if (sub_mask % 41 == h[N - n])

f[n][m] += F(n - 1, sub_mask);

if (sub_mask == 0) break;

}

return f[n][m];

}

Основная часть программы.Читаем входные данные.

scanf("%d %d", &N, &M);

for (i = 0; i < N; i++)

scanf("%d", &h[i]);

memset(f, -1, sizeof(f));

Выводим ответ задачи F(n, 2^m – 1).

printf("%lld\n", F(N, (1 << M) - 1));